Ten artykuł kompleksowo wyjaśnia, jak obliczyć powiększenie soczewki, dostarczając niezbędnych wzorów, definicji i praktycznych przykładów. Dowiesz się, od czego zależy powiększenie, jak stosować równanie soczewki oraz jak interpretować cechy powstającego obrazu, co jest kluczowe dla zrozumienia optyki i zastosowań soczewek w życiu codziennym.
Obliczanie powiększenia soczewki kluczowe wzory i zasady optyki
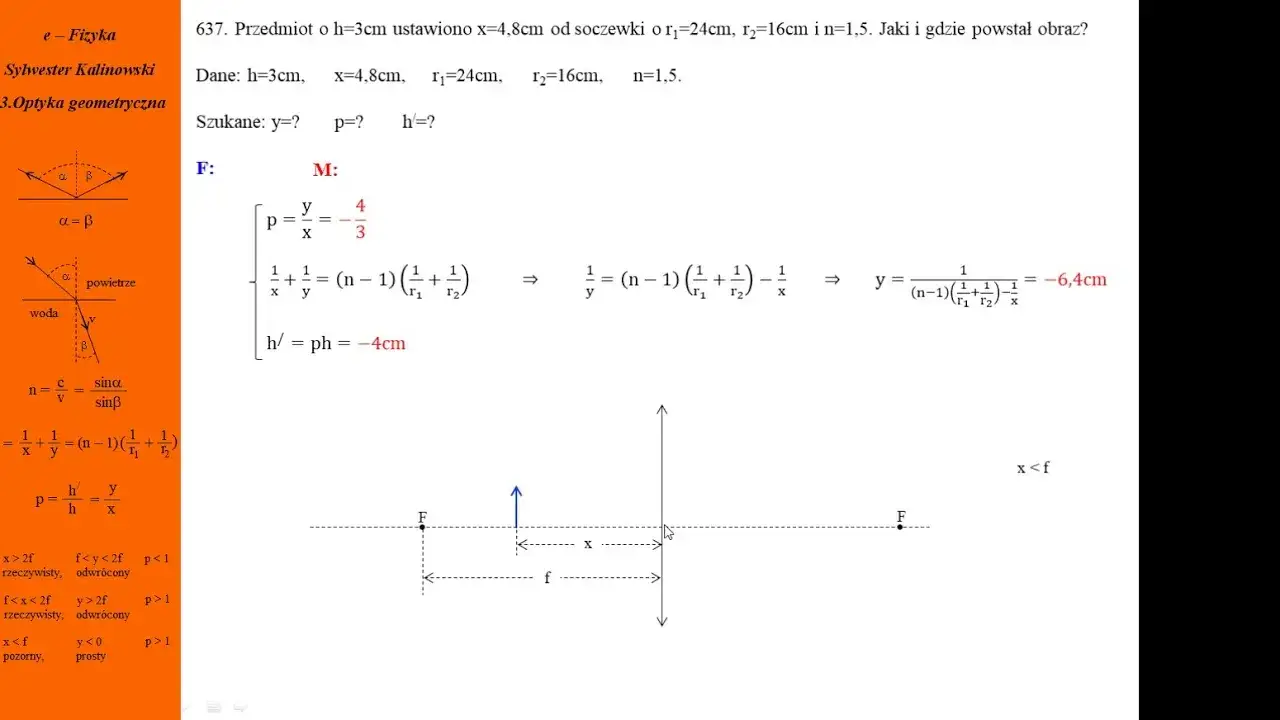
- Powiększenie liniowe (p) to stosunek odległości obrazu do odległości przedmiotu od soczewki (p = |y|/x).
- Równanie soczewki (1/f = 1/x + 1/y) jest podstawą do wyznaczania brakujących danych.
- Dla lupy stosuje się powiększenie kątowe (p_k = d/f), gdzie d to odległość dobrego widzenia (25 cm).
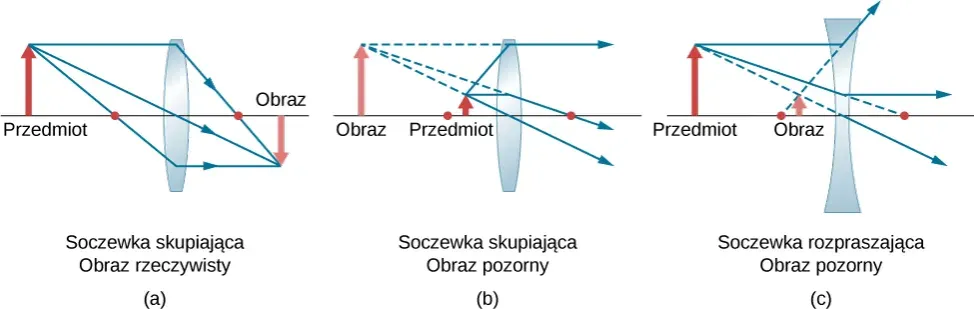
- Soczewki skupiające mogą tworzyć obrazy powiększone lub pomniejszone, rzeczywiste lub pozorne.
- Soczewki rozpraszające zawsze tworzą obrazy pozorne, proste i pomniejszone.
- Wartość powiększenia oraz znak odległości obrazu (y) określają cechy obrazu (wielkość, odwrócenie, rzeczywistość/pozorność).
Od czego zależy powiększenie soczewki? Kluczowe pojęcia, które musisz znać
Z mojego doświadczenia wiem, że zrozumienie powiększenia soczewki zaczyna się od opanowania kilku fundamentalnych pojęć. Powiększenie nie jest wartością stałą dla danej soczewki, ale zależy od konfiguracji optycznej, czyli od tego, jak umieścimy przedmiot względem soczewki. To właśnie te zależności są kluczem do precyzyjnych obliczeń.
Ogniskowa (f) serce każdej soczewki
Ogniskowa (f) to bez wątpienia najważniejszy parametr każdej soczewki. Określa ona jej zdolność do skupiania lub rozpraszania światła. Dla soczewek skupiających (wypukłych) ogniskowa jest zawsze dodatnia, co oznacza, że skupiają one promienie świetlne w jednym punkcie. Z kolei dla soczewek rozpraszających (wklęsłych) ogniskowa jest ujemna, wskazując na ich zdolność do rozpraszania światła. Wartość ogniskowej bezpośrednio wpływa na to, jak duży i jaki rodzaj obrazu soczewka jest w stanie wytworzyć.
Odległość przedmiotu (x) i obrazu (y) gdzie tkwi sekret skali?
Kolejnymi kluczowymi parametrami są odległość przedmiotu od soczewki (x) oraz odległość obrazu od soczewki (y). Odległość przedmiotu (x) to po prostu dystans między przedmiotem a środkiem optycznym soczewki i zawsze przyjmujemy ją jako wartość dodatnią. Odległość obrazu (y) to dystans między obrazem a soczewką. Tutaj sprawa jest nieco bardziej złożona, ponieważ znak 'y' ma fundamentalne znaczenie: dodatnie 'y' oznacza obraz rzeczywisty (powstający po drugiej stronie soczewki), a ujemne 'y' obraz pozorny (powstający po tej samej stronie co przedmiot). Wzajemny stosunek tych dwóch odległości jest bezpośrednio związany z wielkością i położeniem uzyskanego obrazu.
Zdolność skupiająca (dioptrie) a powiększenie jak to się łączy?
Zdolność skupiająca (Z) soczewki to miara jej "mocy" i jest definiowana jako odwrotność ogniskowej wyrażonej w metrach: Z = 1/f. Jednostką zdolności skupiającej są dioptrie (D). Choć zdolność skupiająca nie jest bezpośrednio tożsama z powiększeniem, to jednak pośrednio na nie wpływa. Im większa zdolność skupiająca (czyli im krótsza ogniskowa), tym "silniejsza" soczewka i tym większe powiększenia (lub pomniejszenia) jest w stanie wygenerować w określonych warunkach. Jest to szczególnie ważne w przypadku okularów korekcyjnych, gdzie moc w dioptriach jest podstawowym parametrem.
Jak obliczyć powiększenie liniowe? Niezbędny wzór i praktyczne przykłady
Przejdźmy teraz do sedna, czyli do konkretnych obliczeń. Powiększenie liniowe to najczęściej stosowana miara, gdy chcemy określić, ile razy obraz jest większy lub mniejszy od przedmiotu. Zapewniam, że z odpowiednim wzorem i kilkoma przykładami, stanie się to dla Ciebie jasne.
Podstawowy wzór na powiększenie (p = |y|/x) jak go poprawnie interpretować?
Podstawowy wzór na powiększenie liniowe (p) jest prosty i intuicyjny: p = |y| / x. W tym wzorze 'p' to powiększenie, 'y' to odległość obrazu od soczewki, a 'x' to odległość przedmiotu od soczewki. Używamy wartości bezwzględnej dla 'y', ponieważ powiększenie jako wielkość opisująca stosunek rozmiarów jest zawsze dodatnie. Pamiętaj, że powiększenie jest liczbą niemianowaną, co oznacza, że nie ma jednostek po prostu mówi nam, ile razy coś jest większe lub mniejsze.
Krok po kroku: Obliczanie powiększenia dla soczewki skupiającej
Przyjrzyjmy się praktycznemu przykładowi. Załóżmy, że mamy soczewkę skupiającą o ogniskowej f = 10 cm, a przedmiot umieszczamy w odległości x = 15 cm od niej. Jak obliczyć powiększenie?
- Podaj dane początkowe: Mamy f = 10 cm (soczewka skupiająca, więc f jest dodatnie) i x = 15 cm.
-
Użyj równania soczewki, aby wyznaczyć odległość obrazu (y):
Równanie soczewki to: 1/f = 1/x + 1/y
Podstawiamy znane wartości:
1/10 = 1/15 + 1/y
Przekształcamy, aby wyznaczyć 1/y:
1/y = 1/10 - 1/15
Sprowadzamy do wspólnego mianownika (np. 30):
1/y = 3/30 - 2/30
1/y = 1/30
Zatem, y = 30 cm.
-
Podstaw wyznaczone 'y' oraz znane 'x' do wzoru na powiększenie liniowe (p = |y|/x):
p = |30 cm| / 15 cm
p = 2.
-
Zinterpretuj wynik powiększenia oraz znak 'y':
Otrzymaliśmy p = 2, co oznacza, że obraz jest dwukrotnie powiększony. Ponieważ y = 30 cm (wartość dodatnia), obraz jest rzeczywisty. Dla soczewek skupiających obraz rzeczywisty jest zawsze odwrócony.
Przykład z życia: Obraz tworzony przez projektor
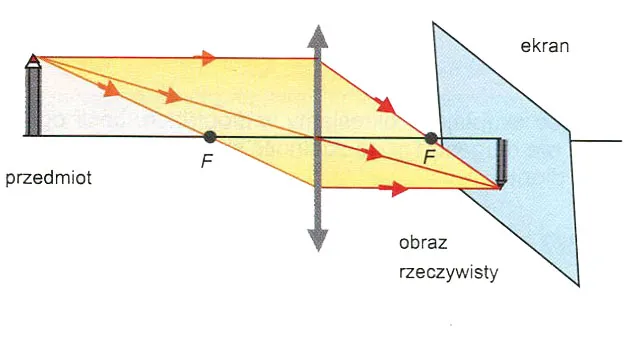
Świetnym przykładem zastosowania soczewek skupiających do tworzenia powiększonego obrazu jest projektor. W projektorze, slajd lub matryca LCD/DLP (przedmiot) jest umieszczony w określonej odległości od soczewki skupiającej. Soczewka ta tworzy na ekranie (który jest w miejscu powstania obrazu) powiększony, rzeczywisty i odwrócony obraz. Obraz jest rzeczywisty, ponieważ powstaje po drugiej stronie soczewki (y > 0) i można go rzutować na ekran. Odwrócenie obrazu jest korygowane przez odpowiednie umieszczenie slajdu lub cyfrową obróbkę obrazu.
Czy soczewka rozpraszająca zawsze pomniejsza? Analiza wzoru
Tak, mogę z całą pewnością stwierdzić, że soczewka rozpraszająca zawsze tworzy obrazy pozorne, proste i pomniejszone (czyli p < 1). Dzieje się tak, ponieważ dla soczewki rozpraszającej ogniskowa (f) jest ujemna. Gdy podstawimy ujemną wartość 'f' do równania soczewki (1/f = 1/x + 1/y), okaże się, że odległość obrazu 'y' zawsze będzie ujemna, co oznacza obraz pozorny. Ponadto, matematycznie wynika z tego, że wartość bezwzględna 'y' zawsze będzie mniejsza od 'x', co prowadzi do powiększenia 'p' zawsze mniejszego od 1. To jest kluczowa różnica w porównaniu do soczewek skupiających.
Równanie soczewki Twoje narzędzie do znalezienia brakujących danych
Równanie soczewki to prawdziwy "szwajcarski scyzoryk" w optyce geometrycznej. Pozwala nam ono na wyznaczenie dowolnej z trzech zmiennych (ogniskowej, odległości przedmiotu lub odległości obrazu), jeśli znamy pozostałe dwie. To właśnie dzięki niemu możemy obliczyć powiększenie, nawet jeśli nie znamy bezpośrednio odległości obrazu.
Jak wyznaczyć odległość obrazu (y), gdy znasz ogniskową i położenie przedmiotu?
Bardzo często w zadaniach lub praktycznych zastosowaniach znamy ogniskową soczewki (f) i odległość, w jakiej umieściliśmy przedmiot (x). Potrzebujemy wtedy odległości obrazu (y), aby obliczyć powiększenie. Z równania soczewki 1/f = 1/x + 1/y możemy łatwo wyznaczyć 'y'. Przekształcając wzór, otrzymujemy:
1/y = 1/f - 1/x
1/y = (x - f) / (f * x)
Zatem, y = (f * x) / (x - f). Ten wzór jest niezwykle przydatny i pozwala szybko obliczyć 'y' bez konieczności każdorazowego sprowadzania do wspólnego mianownika.
Praktyczne zadanie: Oblicz powiększenie, znając tylko f i x
Wyobraźmy sobie, że przedmiot umieścimy w podwójnej ogniskowej soczewki skupiającej. Oznacza to, że x = 2f. Jakie powiększenie uzyskamy?
- Podaj dane: Mamy ogniskową f (dodatnią dla soczewki skupiającej) i odległość przedmiotu x = 2f.
-
Oblicz odległość obrazu (y) za pomocą przekształconego równania soczewki:
y = (f * x) / (x - f)
Podstawiamy x = 2f:
y = (f * 2f) / (2f - f)
y = 2f² / f
y = 2f.
-
Oblicz powiększenie (p) za pomocą wzoru p = |y|/x:
p = |2f| / 2f
p = 1.
-
Zinterpretuj wynik:
Otrzymaliśmy p = 1, co oznacza, że obraz jest tej samej wielkości co przedmiot. Ponieważ y = 2f (wartość dodatnia), obraz jest rzeczywisty i odwrócony. Jest to klasyczny przypadek, często wykorzystywany w demonstracjach optycznych.
Najczęstsze błędy w obliczeniach i jak ich unikać (uwaga na znaki!)
Jako osoba z doświadczeniem w optyce, mogę wskazać kilka pułapek, w które studenci i pasjonaci fizyki najczęściej wpadają. Kluczem do sukcesu jest konsekwencja w stosowaniu konwencji znaków.
- Błędne stosowanie konwencji znaków dla ogniskowej (f): Pamiętaj, że f jest dodatnie dla soczewek skupiających i ujemne dla rozpraszających. To absolutna podstawa. Pomylenie znaku 'f' prowadzi do całkowicie błędnych wyników.
- Niewłaściwa interpretacja znaku odległości obrazu (y): Dodatnie 'y' zawsze oznacza obraz rzeczywisty (powstający po drugiej stronie soczewki, można go rzutować na ekran). Ujemne 'y' oznacza obraz pozorny (powstający po tej samej stronie co przedmiot, nie można go rzutować). Ten znak jest kluczowy dla zrozumienia charakteru obrazu.
- Błędy w jednostkach: Zawsze upewnij się, że wszystkie odległości (f, x, y) są wyrażone w tych samych jednostkach. Jeśli ogniskowa jest w centymetrach, to 'x' i 'y' również powinny być w centymetrach. Mieszanie jednostek (np. metry i centymetry) jest prostą drogą do błędnych obliczeń.
Nie tylko wielkość ma znaczenie Jak określić cechy obrazu na podstawie obliczeń?
Obliczenie samego powiększenia to dopiero początek. Prawdziwe zrozumienie optyki polega na umiejętności zinterpretowania wyników i określenia wszystkich cech powstałego obrazu. To właśnie one mówią nam, czy obraz jest użyteczny, czy też nie.
Powiększony, pomniejszony czy rzeczywisty? Co mówi nam wartość "p"?
Wartość liczbowa powiększenia 'p' dostarcza nam bezpośredniej informacji o rozmiarze obrazu w stosunku do przedmiotu:
- Jeśli p > 1, obraz jest powiększony. Jest większy niż przedmiot.
- Jeśli p = 1, obraz jest tej samej wielkości co przedmiot.
- Jeśli 0 < p < 1, obraz jest pomniejszony. Jest mniejszy niż przedmiot.
To proste kryterium pozwala nam szybko ocenić skalę obrazu.
Obraz prosty czy odwrócony? Rola znaku przy odległości obrazu (y)
Jak już wspomniałem, znak odległości obrazu (y) jest niezwykle ważny. W większości przypadków optyki soczewek:
- Jeśli y jest dodatnie (obraz rzeczywisty), obraz jest zazwyczaj odwrócony względem przedmiotu. Oznacza to, że jeśli przedmiot stoi pionowo, jego obraz będzie stał "do góry nogami".
- Jeśli y jest ujemne (obraz pozorny), obraz jest zazwyczaj prosty (nieodwrócony) względem przedmiotu.
Ta zależność jest kluczowa przy projektowaniu przyrządów optycznych, gdzie orientacja obrazu ma znaczenie.
Obraz rzeczywisty a pozorny kluczowa różnica, którą musisz zrozumieć
Rozróżnienie między obrazem rzeczywistym a pozornym to podstawa. Poniższa tabela jasno przedstawia najważniejsze różnice, które pomogą Ci w interpretacji wyników obliczeń:
| Cecha | Obraz Rzeczywisty | Obraz Pozorny |
|---|---|---|
| Możliwość rzutowania na ekran | Tak | Nie |
| Sposób powstawania | Przecięcie rzeczywistych promieni świetlnych | Przecięcie przedłużeń promieni świetlnych |
| Znak odległości obrazu (y) | Dodatni (y > 0) | Ujemny (y < 0) |
| Odwrócenie | Zazwyczaj odwrócony | Zazwyczaj prosty |
Zrozumienie tych różnic jest fundamentalne dla każdego, kto chce zgłębić tajniki optyki.
A co z lupą? Jak obliczyć powiększenie kątowe?
Kiedy mówimy o lupach, mikroskopach czy teleskopach, powiększenie liniowe przestaje być jedyną i najważniejszą miarą. Wkracza tu koncepcja powiększenia kątowego, która lepiej oddaje to, jak postrzegamy powiększenie przez takie przyrządy.
Dlaczego dla lupy używamy innego wzoru? Koncepcja powiększenia kątowego
Dla lupy i innych przyrządów optycznych, które służą do obserwacji obiektów bezpośrednio przez soczewkę (bez rzutowania obrazu na ekran), ważniejsze jest powiększenie kątowe (p_k). Dzieje się tak, ponieważ percepcja wielkości obiektu przez ludzkie oko zależy od kąta, pod jakim obiekt jest widziany. Lupa sprawia, że obiekt wydaje się większy, ponieważ widzimy go pod większym kątem. W obliczeniach powiększenia kątowego często odwołujemy się do tzw. odległości dobrego widzenia (d), która standardowo wynosi 25 cm. Jest to odległość, z której większość ludzi jest w stanie komfortowo i wyraźnie widzieć drobne szczegóły.
Wzór p_k = d/f jak go zastosować w praktyce?
Wzór na powiększenie kątowe dla lupy jest bardzo prosty: p_k = d/f. W tym wzorze 'd' to odległość dobrego widzenia (zazwyczaj 25 cm), a 'f' to ogniskowa lupy. Ważne jest, aby 'd' i 'f' były wyrażone w tych samych jednostkach (np. oba w centymetrach), aby wynik był poprawny. Powiększenie kątowe, podobnie jak liniowe, jest liczbą niemianowaną.
Przykład: Jakie powiększenie da lupa o ogniskowej 4 cm?
Obliczmy powiększenie kątowe dla typowej lupy o ogniskowej 4 cm:
- Podaj dane: Odległość dobrego widzenia d = 25 cm, ogniskowa lupy f = 4 cm.
- Zastosuj wzór na powiększenie kątowe: p_k = d/f.
-
Wykonaj obliczenie i podaj wynik:
p_k = 25 cm / 4 cm
p_k = 6.25.
Oznacza to, że lupa o ogniskowej 4 cm powiększa obraz około 6.25 razy.
Przeczytaj również: Soczewki kontaktowe: Gdzie kupić, by nie żałować? Pełny przewodnik
Powiększenie w okularach czy "plusy" naprawdę powiększają świat?
Na koniec chciałbym poruszyć kwestię powiększenia w kontekście okularów korekcyjnych, ponieważ często spotykam się z błędnym przekonaniem, że okulary "powiększają" lub "pomniejszają" świat.
Główna rola soczewki okularowej korekcja, nie powiększanie
Muszę jasno podkreślić, że głównym zadaniem soczewek okularowych nie jest powiększanie obiektów, lecz korekcja wad wzroku. Ich celem jest odpowiednie skupianie światła na siatkówce oka, aby obraz był ostry i wyraźny. Soczewki w okularach mają określoną moc wyrażoną w dioptriach, która jest kluczowym parametrem korekcyjnym, a nie miarą powiększenia w sensie lupy.
Skąd bierze się efekt "dużych oczu" u osób z nadwzrocznością?
Mimo że okulary nie są przeznaczone do powiększania, osoby z dużą nadwzrocznością, noszące okulary z soczewkami skupiającymi (tzw. "plusami"), mogą zauważyć efekt "dużych oczu" widzianych przez ich okulary. Dzieje się tak, ponieważ soczewki skupiające, umieszczone blisko oka, tworzą pozorny, powiększony obraz oka dla obserwatora z zewnątrz. To zjawisko jest efektem ubocznym właściwości optycznych soczewek skupiających i ich interakcji ze światłem przechodzącym przez oko, a nie celowym powiększeniem obrazu świata dla osoby noszącej okulary.